
Translation Agency | Email US | Translation Resources | Translation Jobs | Translation Agencies
World Languages | Translation Tips | Translation Services
Translations of
Encyclopedia by Czech and Slovak to English translator

Translation Agency |
Email US |
Translation
Resources | Translation Jobs | Translation Agencies
World Languages | Translation Tips | Translation Services
Around 2000 B.C., the Babylonians and Egyptians were already interested in calculating integrals (derived from the Latin word of integral, meaning whole). They also knew how to calculate objects and quadratic
frustums, and the Babylonians knew how to calculate the volume of frustums.One of Platonís students, the Greek Eudoxos from Kine (408 - 355 B.C.), thought up the dateless method of calculating with which it was possible to solve integral calculation problems without the use of integration. Using his method, quadrates could be craftily determined using
proportional references. This procedure is presently referred to as an exhaustation method and he was the first to set critical values. The Greek Euclides (about 365 - 300 B.C.) used this method when calculating spires and the famous Archimedes (287 - 212 B.C.) used it to calculate circles, spirals, parabolas and spheres.The advancement of integral calculus was renewed after a long period when Michael Stifel (1487 - 1567) discovered irrational numbers. When studying curves and curved surfaces, the Jezuit Bonaventure Cavalier (1598 - 1647) arrived at the concept of indivisibility and, using this "indivisible geometry", attempted to describe surfaces and objects, as such arriving at the step just before integral calculus. The French lawyer and amateur mathematician Pierre de Fermat (1601 - 1665) was able to expound on this further with his first calculation of the surfaces of parabolas, spirals and hyperbolas using outline procedures.
French mathematician Blaise Pascal (1623-1662) and English mathematician Jogn Wallis (1616-1703) expanded on this thought. Wallis introduced the symbol of infinity and was the first to attempt to interpret imaginary numbers using geometry. Two famous mathematicians, Gottfried W. Leibnitz (1646-1716) and Isaac Newton (1643-1727), recognised that integral calculus is essentially the opposite of differential calculus. Leibnitzís genial symbol for this clearly reflects this concept.
What does the opposite of integral and differential calculus mean? Physicists and engineers have attempted to use differential calculus to determine certain points on curves, speed, ascent and other factors, measuring the differences by experiment. However, experimenting physicists have a reverse approach, seeking functions whose differential quotients give the desired values in an experiment. Such functions are called integrals. If differential calculus came about from problems relating to tangents, then integral calculus came about from
quadrature problems, which means the content of some curve bordering a surface should be determined. The concept of quadrature is associated above all to the notions of ancient Greeks, who considered surfaces as computable if they could be spread out on a square. This brings us back to the previously mentioned exhaustation method.We can easily understand the basic notion of integral calculus if we think "geometrically". Integration as a calculation operation is concerned with how to assign a previously given function a fixed numerical value or other function. This is understood as an indefinite integral, which concerns the content of a surface, bordered by the curve y = F(X), an x axis of a coordinal system, and the ordinates a and b. We write an indefinite integral in the following manner:
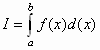
where f(x) is referred to as the integrand, I as the integral, the interval (a,b) as the integration limit, and the variable x as the integration variable. Because we are defining a surface, we can refer to I as F(x). The calculation of the surface is accomplished by dividing the surface between the upper and lower boundaries using a series of ordinates in parallel intervals into two different types of rectangles.
![]() <
F
<
F
<F
![]()
The difference between both sums of rectangles
is the defined surface and is smaller the smaller is ![]() .
If
.
If ![]() approaches the value of 0,
then both sums equal one another and will equal the defined surface. If the
function F(x) has one constant C, meaning F(x) + C, then a constant factor may
be written before the integral symbol:
approaches the value of 0,
then both sums equal one another and will equal the defined surface. If the
function F(x) has one constant C, meaning F(x) + C, then a constant factor may
be written before the integral symbol:
![]()
The sum of several addends can be integrated by parts, expressed by the following formula:
![]()
Furthermore, there also exists partial
integration, which is understood as the conversion of one integral into another,
usually a more simple one. An integrand is understood as a function which
represents the sum of two other functions. The rule of quotients during
derivation can be inversed, although this only has significance in a few
particular examples. It is also possible to perform integration by substitution
if ![]() is a function of
is a function of
![]() and if
and if ![]() exists. It generally
applies that every consecutive function is integratable. Integrals which can be
expressed using elementary functions are referred to in analysis as new and
higher but not elementary functions. Most often, an integrand is converted into
a series, whose individual terms are integrated while it is understood that an
unlimited series is convergent in equal intervals and that each of the terms is
integratable. The series then converges by integrating the individual terms. If
the limits of an integral are interchanged, the sign before the integral also
changes.
exists. It generally
applies that every consecutive function is integratable. Integrals which can be
expressed using elementary functions are referred to in analysis as new and
higher but not elementary functions. Most often, an integrand is converted into
a series, whose individual terms are integrated while it is understood that an
unlimited series is convergent in equal intervals and that each of the terms is
integratable. The series then converges by integrating the individual terms. If
the limits of an integral are interchanged, the sign before the integral also
changes.
If instead of a fixed limited integral a, b we choose some upper limit, we are referring to an indefinite integral, calculated in the following manner:
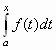 or
or
![]()
Translating German French Translations French German Translating Polish German Translations English French Translating Polish
Translation Agency |
Email US |
Translation
Resources | Translation Jobs
Translation Agencies | World Languages | Translation Tips | Translation Services

Copyright © KENAX, by Karel Kosman - All Rights Reserved Worldwide.