Translations of Encyclopedia about Mathematics

Binomial Functions

This concept is part of the calculus of probabilities. So that we can understand it, it is necessary to work with calculus of probabilities. We can get through binomial functions like across some bridge, from the most simplest of probability theses to concepts covering polynomes.

A refers to the fact that some randomly selected product manufactured by a factory is waste (a faulty product). Three samples of output are meant to be selected from production and meant to be part of a larger experiment. If, with each attempt, we are only interested in the occurrence of event A, then, with the larger experiment, we can label three other events B1, B2, B3 with each sample drawn. Therefore, there are a total of eight basic possible outcomes:

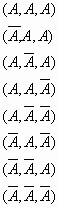
which means that, with the first and third attempts, we would always get the event and, with the second attempt, A. Let us make the following assumptions:

the probability that a sample product will be faulty is a constant value of p = P (A) with all of the individual sets;
the results of each sample are entirely independent of one another.

From these two assumptions, some formulas relating to special cases arise when P () = 1- p. A random experiment, during which event A can occur, is repeated n times. Let Ai be a result when, during a series of attempts, the sample event A occurs during the ith attempt. In this case, we would call a series of samples or attempts of number n as a Bernoullian attempt if the most important conditions were fulfilled.

The concept of Bernoulli’s experiment was introduced in honour of mathematician Jacob Bernoulli, who is closely associated with binomial divisions. If we perform some random experiment n times and in which there are only two possible outcomes, success or failure, while none of the results influence each other, we are referring to a Bernoullian experiment.

In the previous example, let S_k "tge result of a series of samples of the number 3, when event A occurred k times" for k = 0,1,2,3. According to theorem 1. It applies that event A occurs with a probability of p = P (). Therefore, for a probability of p_k it applies that a Bernoullian attempt of extent n, event A occurs exactly k times. Proof: using S_k, we mark event A, which occurs exactly k times in a series of n attempts. From this we can say that S_k always occurs whenever A occurs during the first k attempts, and during the remaining n-k attempts when A occurs.

According to this, we can recognise that we are dealing with a Bernoullian experiment. Each subsequent occurrence of S_k can take place through permutation, where each permutation has the same probability. In conclusion, we can say there exists many types of this kind of permutation and from which the assertion of results ensues. The probability p_k represents terms in the binomial expansion of (p + (1-p))ⁿ. From this we derive the name of binomial division.

Binomial samples serve to solve binomes.

Binomial samples are used in the most varied of mathematics fields, such as when computing probabilities and for analyses, making them a useful instrument for solving quadratic equations. Note that these are binomes of the second order, given in the form:

(a + b)², where a, b Î R.

From the general binomial theorem, we get three binomial samples for a second order binome.

The first binomial formula:

(a + b)² = a² + 2ab + b², where a, b Î R.

The second binomial formula:

(a – b)² = a² – 2ab + b², where a, b Î R.

Third binomial formula:

(a + b)(a – b) = a² – b², where a, b Î R.

Using these three formulas, we are often able to quickly deduce a solution for quadratic equations. For example:

We are given the quadratic equation:

x² + 8x = - 16

which we can transform to achieve:

x²+ 8x + 16 = 0

and, using the first binomial formula, we end up with

(x + 4)² = 0

by extracting the left hand side, we achieve the solution S = { -4}

Translating Dutch Hungarian Translations Hungarian Dutch Translating Swedish Czech Translations Czech Swedish Translating Russian