Translations of Encyclopedia about Mathematics

Principles of Computing with Powers

For a base number a and its power, the following applies:

For a ¹ 0 a0 = 1

Which means that, if we exponentiate any number other than zero by the number of zero, its power equals 1.

For n Î A 0n = 0

Or, if we exponentiate the number zero by any natural exponent, its power equals 0.

Adding and Subtracting Powers

2x² + 3x² = 5x² 5y² – 4y² = y²

When adding or subtracting the same valued powers, the coefficients are added and the exponents remain the same. However, it is necessary to make sure that the base numbers are the same (x and y) because, if not, it would not be possible to add or subtract the following:

2x² + 3a² 8y³ - 4x³

The exponents must also be the same, in which case the following could also not be consolidated or simplified:

4x² + 7x³ 6y² - 2y4

Multiplying Powers

Powers with same base numbers and different exponents:

xn · yn = (x · y)n

If we multiply two powers with the same base number and same exponent, we multiply the base numbers and exponentiate the result by the same exponent, such as:

2³ · 4³ = (2 · 4)³ = 8³ = 512

2. Powers with the same base numbers but different exponents:

xn · xm = xn+m

If we multiply two powers with the same base values but with different exponents, the base numbers remain the same but the exponents are added, which gives it a new exponent, applied to the base number. For example:

5² · 5³ = 52+3 = 55 = 3125

Dividing Powers

Powers with different base numbers but same exponents:

xn : yn = (x : y)n

If we divide two powers with different base numbers but same exponents, the base numbers are multiplied and given the original exponent. For example:

28³ : 4³ = (28 : 4)³ = 7³ = 343

2. Powers with the same base number but different exponents:

xm : xn = xm-n

If we divide two powers with the same base value but different exponents, the base numbers remain the same but the exponents subtract from one another, the difference becoming the new exponent. For example:

58 : 56 = 58-6 = 5² = 25

Exponentiating Fractions

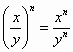
When exponentiating fractions, the nominators and denominators are exponentiated with the same exponent and the result is divided. For example:

Powers with Negative Exponents

For x > 0, it applies that:

Exponentiating Powers

(xm)n = xm·n

When we exponentiate a power, the base number remains the same and the individual exponents are multiplied, their total becoming the new exponent. For example:

(7³)4 = 73·4 = 712 = 13 841 287 201

Extraction of Root

With positive numbers, extraction of root is the opposite of exponentiation.

Equations with extraction of roots have the following form:

where

x is the radical quantitor or the base of the root
n is the exponent of the root
y the result of the extraction of root

is the mathematical symbol for root

The square or second root has an exponent of 2, which may be assumed and need not be stated above the root symbol, as such:

- read as the square root of 25. If the exponent of the root is not equal to 2, it must be stated.

read as the fourth root of 256.

The laws for adding with roots is similar to the laws of adding with powers. The root can also be written as a power with an exponent converted into a fraction, where the exponent of the original root becomes the denominator of the fraction.

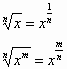
Example:

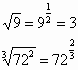
When extracting roots, the following rules should be adhered to:

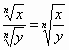
Example:

Translating Russian Ukrainian Translations Ukrainian Russian Translating Persian Arab Translations Arab Persian Translating Turkish