Performance Characteristics
Discharge Curves
Energy
cells have been developed for a wide range of applications using a
variety of different technologies, resulting in a wide range of
available performance characteristics. The graphs below show some of
the main factors an applications engineer should take into account when
specifying a battery to match the performance requirements of the end
product.
Cell Chemistry
The
nominal voltage of a galvanic cell is fixed by the electrochemical
characteristics of the active chemicals used in the cell, the so called
cell chemistry. The actual voltage appearing at the terminals at any
particular time, as with any cell, depends on the load current and the
internal impedance of the cell and this varies with, temperature, the
state of charge and with the age of the cell.
The
graph below shows typical discharge discharge curves for cells using a
range of cell chemistries when discharged at 0.2C rate. Note that each
cell chemistry has its own characteristic nominal voltage and discharge
curve. Some chemistries such as Lithium Ion have a fairly flat
discharge curve while others such as Lead acid have a pronounced slope.
The
power delivered by cells with a sloping discharge curve falls
progressively throughout the discharge cycle. This could give rise to
problems for high power applications towards the end of the cycle. For
low power applications which need a stable supply voltage, it may be
necessary to incorporate a voltage regulator if the slope is too steep.
This is not usually an option for high power applications since the
losses in the regulator would rob even more power from the battery.
A
flat discharge curve simplifies the design of the application in which
the battery is used since the supply voltage stays reasonably constant
throughout the discharge cycle. A sloping curve facilitates the
estimation of the State of Charge of the battery since the cell voltage
can be used as a measure of the remaining charge in the cell. Modern
Lithium Ion cells have a very flat discharge curve and other methods
must be used to determine the State of Charge
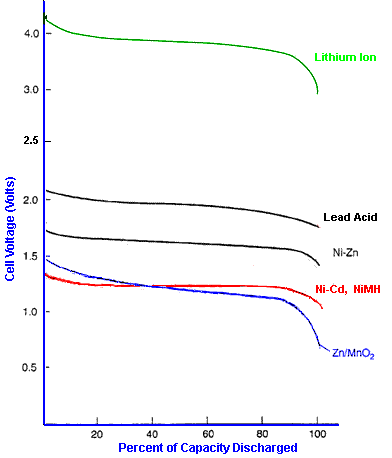
The X axis shows the cell characteristics normalised as a percentage of
cell capacity so that the shape of the graph can be shown independent
of the actual cell capacity. If the X axis was based on discharge time,
the length of each discharge curve would be proportional to the nominal
capacity of the cell.
Temperature Characteristics
Cell
performance can change dramatically with temperature. At the lower
extreme the electrolyte may freeze setting a lower limit on the
operating temperature, while at the upper extreme the active chemicals
may break down destroying the battery. In between these limits the cell
performance generally improves with temperature. See also Thermal Management and Battery Life for more details.
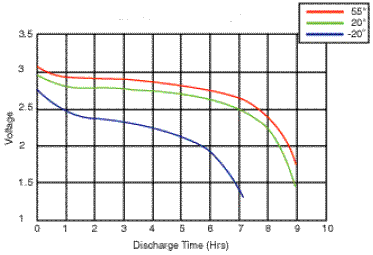
The above graph shows how the performance of Lithium Ion batteries deteriorates as the operating temperature decreases.
Self Discharge Characteristics
The self discharge rate is a measure of how quickly a cell will lose
its energy while sitting on the shelf due to unwanted chemical actions
within the cell. The rate depends on the cell chemistry and the
temperature.
Cell Chemistry
The following shows the typical shelf life for some primary cells:
- Zinc Carbon (Leclanché) 2 to 3 years
- Alkaline 5 years
- Lithium 10 years or more
Typical self discharge rates for common rechargeable cells are as follows:
- Lead Acid 4% to 6% per month
- Nickel Cadmium 15% to 20% per month
- Nickel Metal Hydride 30% per month
- Lithium 2% to 3% per month
Temperature Effects
The
rate of unwanted chemical reactions which cause internal current
leakage between the positive and negative electrodes of the cell, like
all chemical reactions, increases with temperature thus increasing the
battery self discharge rate. See also Battery Life . The graph below shows typical self discharge rates for a Lithium Ion battery.
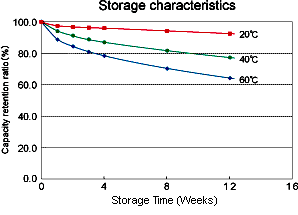
Internal Impedance
The internal impedance of a cell determines its current carrying capability. A low internal resistance allows high currents.
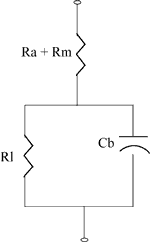
Battery Equivalent Circuit
The diagram on the right shows the equivalent circuit for an energy cell.
- Rm is the resistance of the metallic path through the cell including the terminals, electrodes and inter-connections.
- Ra is the resistance of the electrochemical path including the electrolyte and the separator.
- Cb is the capacitance of the parallel plates which form the electrodes of the cell.
- Ri is the non-linear contact resistance between the plate or electrode and the electrolyte.
Typical internal resistance is in the order of milliohms.
Effects of Internal Impedance
When
current flows through the cell there is an IR voltage drop across the
internal resistance of the cell which decreases the terminal voltage of
the cell during discharge and increases the voltage needed to charge
the cell thus reducing its effective capacity as well as decreasing its
charge/discharge efficiency. Higher discharge rates give rise to higher
internal voltage drops which explains the lower voltage discharge
curves at high C rates. See "Discharge Rates" below.
The
internal impedance is affected by the physical characteristics of the
electrolyte, the smaller the granular size of the electrolyte material
the lower the impedance. The grain size is controlled by the cell
manufacturer in a milling process.
Spiral construction
of the electrodes is often used to maximise the surface area and thus
reduce internal impedance. This reduces heat generation and permits
faster charge and discharge rates.
The
internal resistance of a galvanic cell is temperature dependent,
decreasing as the temperature rises due to the increase in electron
mobility. The graph below is a typical example.
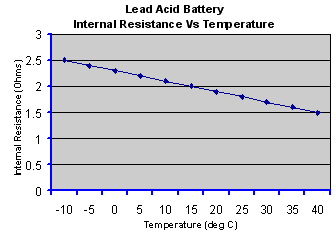
Thus
the cell may be very inefficient at low temperatures but the efficiency
improves at higher temperatures due to the lower internal impedance,
but also to the increased rate of the chemical reactions. However the
lower internal resistance unfortunately also causes the self discharge
rate to increase. Furthermore, cycle life deteriorates at high
temperatures. Some form of heating and cooling may be required to
maintain the cell within a restricted temperature range to achieve the
optimum performance in high power applications.
The
internal resistance of most cell chemistries also tends to increase
significantly towards the end of the discharge cycle as the active
chemicals are converted to their discharged state and hence are
effectively used up. This is principally responsible for the rapid drop
off in cell voltage at the end of the discharge cycle.
In addition the Joule heating effect of the I2R losses in the internal resistance of the cell will cause the temperature of the cell to rise.
The voltage drop and the I2R
losses may not be significant for a 1000 mAh cell powering a mobile
phone but for a 100 cell 200 Ah automotive battery they can be
substantial. Typical internal resistance for a 1000mA Lithium mobile
phone battery is around 100 to 200mOhm and around 1mOhm for a 200Ah
Lithium cell used in an automotive battery.
Operating
at the C rate the voltage drop per cell will be about 0.2 volts in both
cases, (slightly less for the mobile phone). The I2R loss in
the mobile phone will be between 0.1 and 0.2 Watts. In the automotive
battery however the voltage drop across the whole battery will be 20
Volts and I2R power loss dissipated as heat within the
battery will be 40 Watts per cell or 4KW for the whole battery. This is
in addition to the heat generated by the elecrochemical reactions in
the cells.
As
a cell ages, the resistance of the electrolyte tends to increase. Aging
also causes the surface of the electrodes to deteriorate and the
contact resistance builds up and at the same the effective area of the
plates decreases reducing its capacitance. All of these effects
increase the internal impedance of the cell adversely affecting its
ability to perform. Comparing the actual impedance of a cell with its
impedance when it was new can be used to give a measure or
representation of the age of a cell or its effective capacity. Such
measurements are much more convenient than actually discharging the
cell and can be taken without destroying the cell under test. See "Impedance and Conductance Testing"
The
internal resistance also influences the effective capacity of a cell.
The higher the internal resistance, the higher the losses while
charging and discharging, especially at higher currents. This means
that for high discharge rates the lower the available capacity of the
cell. Conversely, if it is discharged over a prolonged period, the
AmpHour capacity is higher. This is important because some
manufacturers specify the capacity of their batteries at very low
discharge rates which makes them look a lot better than they really
are.
Discharge Rates
The
discharge curves for a Lithium Ion cell below show that the effective
capacity of the cell is reduced if the cell is discharged at very high
rates (or conversely increased with low discharge rates). This is
called the capacity offset and the effect is common to most cell
chemistries.
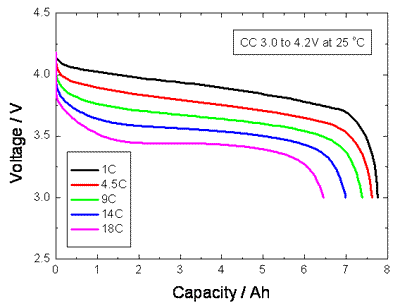
If
the discharge takes place over a long period of several hours as with
some high rate applications such as electric vehicles, the effective
capacity of the battery can be as much as double the specified capacity
at the C rate. This can be most important when dimensioning an
expensive battery for high power use. The capacity of low power,
consumer electronics batteries is normally specified for discharge at
the C rate whereas the SAE uses the discharge over a period of 20 hours
(0.05C) as the standard condition for measuring the Amphour capacity of
automotive batteries. The graph below shows that the effective capacity
of a deep discharge lead acid battery is almost doubled as the
discharge rate is reduced from 1.0C to 0.05C. For discharge times less
than one hour (High C rates) the effective capacity falls off
dramatically.
The
effectiveness of charging is similarly influenced by the rate of
charge. An explanation of the reasons for this is given in the section
on Charging Times .
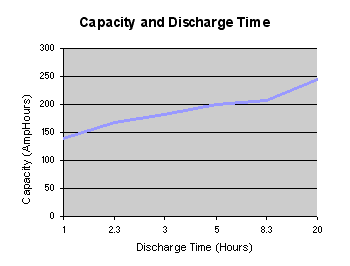
There are two conclusions to be drawn from this graph:
- Care should be exercised when comparing battery capacity specifications to ensure that comparable discharge rates are used.
- In
an automotive application, if high current rates are used regularly for
hard acceleration or for hill climbing, the range of the vehicle will
be reduced.
Notes: For information
- A
typical small electric car will use between 150 to 250 Watthours of
energy per mile with normal driving. Thus, for a range of 100 miles at
200 Watthours per mile, a battery capacity of 20 KWh will be required.
- Hybrid
electric vehicle use smaller batteries but they may be required to
operate at very high discharge rates of up to 40C. If the vehicle uses
regenerative braking the battery must also accept very high charging
rates to be effective. See the section about Capacitors for an example of how this requirement can be accommodated.
Peukert Equation
The
Peukert equation is a convenient way of characterising cell behaviour
and of quantifying the capacity offset in mathematical terms.
This
is an empirical formula which approximates how the available capacity
of a battery changes according to the rate of discharge. C = I n
T where "C" is the theoretical capacity of the battery expressed in amp
hours, "I" is the current, "T" is time, and "n" is the Peukert Number,
a constant for the given battery. The equation shows that at higher
currents, there is less available energy in the battery. The Peukert
Number is directly related to the internal resistance of the battery.
Higher currents mean more losses and less available capacity.
The
value of the Peukert number indicates how well a battery performs under
continuous heavy currents. A value close to 1 indicates that the
battery performs well; the higher the number, the more capacity is lost
when the battery is discharged at high currents. The Peukert number of
a battery is determined empirically. For Lead acid batteries the number
is typically between 1.3 and 1.4
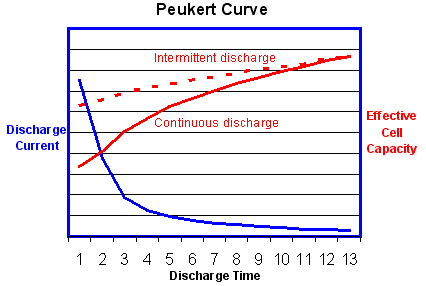
The
graph above shows that the effective battery capacity is reduced at
very high continuous discharge rates. However with intermittent use the
battery has time to recover during quiescent periods when the
temperature will also return towards the ambient level. Because of this
potential for recovery, the capacity reduction is less and the
operating efficiency is greater if the battery is used intermittently
as shown by the dotted line.
Note
that this is the reverse of the behaviour of an internal combustion
engine which operates most efficiently with continuous steady loads. In
this respect electric power is a better solution for delivery vehicles
which are subject to continuous interruptions.
Ragone Plot
The
Ragone plot is another way of characterising the reduction in effective
capacity or capacity offset as the discharge rate (or power delivered)
is increased. The graph below also useful for demonstrating the
superior gravimetric energy density of Lithium Ion cells.
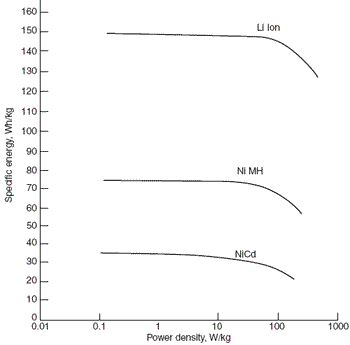
Similar graphs can be plotted for the volumetric energy density.
See also Alternative Energy Storage Comparisons.
Cycle Life
This is one of the key cell performance parameters and gives an indication of the expected working lifetime of the cell.
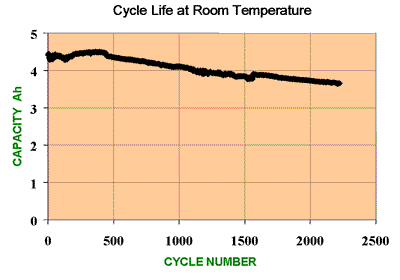
The
cycle life is defined as the number of cycles a cell can perform before
its capacity drops to 80% of its initial specified capacity.
Note
that the cell does not die suddenly but continues a slow deterioration
which will be almost imperceptible to the user. At the end of the
specified cycle life the cell will continue to function normally except
that its capacity will be significantly less than it was when it was
new.
The
cycle life as defined is a useful way of comparing batteries under
controlled conditions, however it may not give the best indication of
battery life under actual operating conditions. Cells are seldom
operated under successive, complete charge - discharge cycles, they are
much more likely to be subject to partial discharges of varying depth
before complete recharging. Since smaller amounts of energy are
involved in partial discharges, the battery can sustain a much greater
number of shallow cycles. Such usage cycles are typical for Hybrid
Electric Vehicle applications with regenerative braking. See how cycle
life varies with depth of discharge in Battery Life
A more representative measure of battery life is the Lifetime Energy Throughput.
This is the total amount of energy in Watthours which can be taken out
of a battery over all the cycles in its lifetime before its capacity
reduces to 80% of its initial capacity when new. Unfortunately this
measure is not yet in common use by cell manufacturers and has not yet
been adopted as a battery industry standard. Until it comes into
general use it will not be possible to use it to compare the
performance of cells from different manufacturers in this way but, when
available, at least it provides a more useful guide to applications
engineers for estimating the useful life of batteries used in their
designs.
Deep Discharge
Cycle life decreases with increased Depth of Discharge (DOD) (See Battery Life)
and many cell chemistries will not tolerate deep discharge and cells
may be permanently damaged if fully discharged. Special cell
constructions and chemical mixes are required to maximise the potential
DOD of deep cycle batteries.
Charging Characteristics
Charging curves and recommended charging methods are included in a separate section on Charging
|